Dynamic Tire Friction Potential

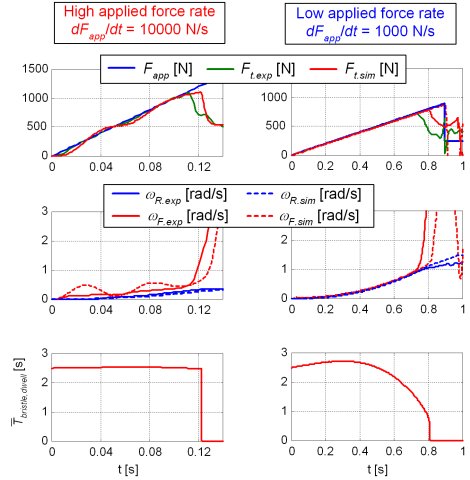
Traction control systems/ABS are aimed to keep the longitudinal tire force at the maximum static friction potential level, thus providing maximum acceleration/deceleration. The experimental results obtained by using the experimental electrical vehicle with in-wheel motor, which are shown in Fig. 1, indicate that the longitudinal tire force during abrupt wheel torque transients on ice surface can be several times larger than the static potential. This effect has been named Dynamic Tire Friction Potential (DTFP).

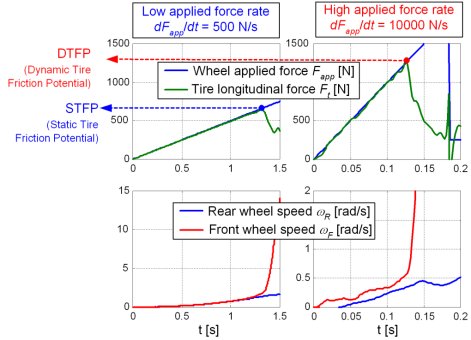
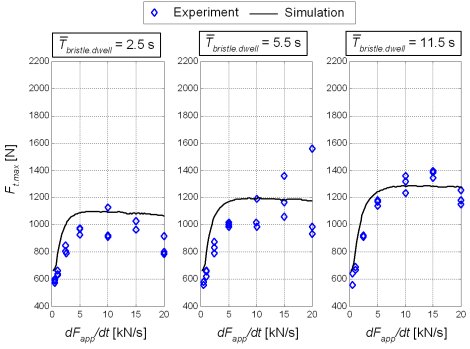
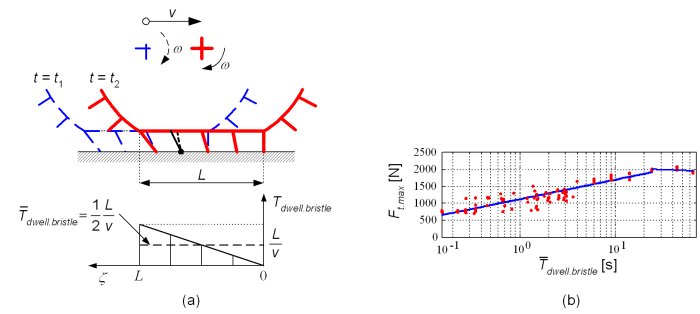
Fig. 2 shows the DTFP values for ice arena tests and various operating parameters. The DTFP significantly grows with increase of the applied force (torque) rate in the range dF_app/dt < 15000 N/s. The DTFP is further boosted if the tire dwells on ice surface for some time before the abrupt transient occurs, which is explained by the tire-ice imprinting effect. The DTFP is present at small vehicle speeds only.

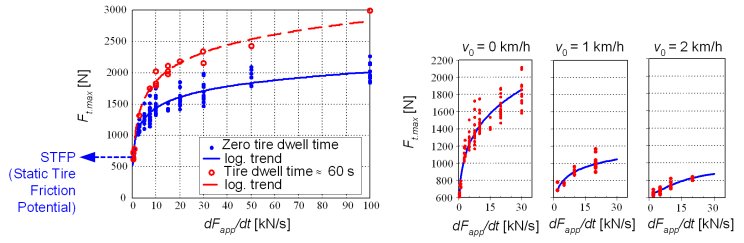
**Fig. 2.** DTFP dependence on applied force rate, tire dwell time, and initial vehicle speed.

Based on the observed dwell time influence and the brush tire model in Fig. 3a, it has been hypothesized that the DTFP dependencies on the vehicle speed and the applied force rate come from the bristle dwell time effect. Even for the zero tire dwell time, the bristle dwell time in the tire-road contact patch is larger than zero. The larger the vehicle velocity the lower the average bristle dwell time, and the lower the DTFP. Also, for smaller applied force rates the tire rolls away from its initial contact patch, thus loosing the bristle dwell time and the DTFP. Fig. 3b shows that the average bristle dwell time of a couple of seconds is long enough to significantly boost the DTFP.

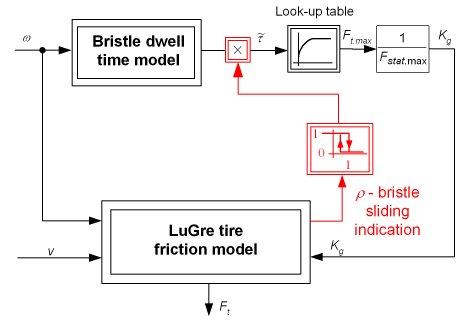
**Fig. 3.** Illustration of DTFP dependence on average bristle dwell time.

Based on the above bristle dwell time hypothesis, the DTFP behavior has been described by the tire friction dynamics model shown by the principal block diagram in Fig. 4. The previously developed distributed-parameter LuGre tire frcition model is extended by a distributed-parameter bristle dwell time model to capture the DTFP effect. A lumped-parameter version of the model has been developed, as well. The average bristle dwell time is used to schedule the maximum static friction force. If a bristle starts to slide, its dwell time state variable is reset to zero ( = 0). Similarly, the dwell time state should be reset if the rolling tire transfers a longitudinal force (not shown in Fig. 4).

**Fig. 4.** Principal block diagram of tire friction dynamics model including DTFP effect.

The experimental validation results in Figs. 5 and 6 indicate that the proposed tire friction dynamics model (Fig. 4) can accurately predict the abrupt tire transient response and the related DTFP vs. applied force rate curve.

**Fig. 5.** Validation results in time domain.

**Fig. 6.** DTFP-characteristic validation results.