Modeling of Hydrostatic Transmission
An attractive alternative to traditional clutch-actuated active differentials is an active (torque vectoring) differential based on hydrostatic transmission actuation. The main benefits of hydrostatic active differentials include superior thermal capacity, durability, and efficiency. For the purpose of active differential dynamics research, a control-oriented mathematical model of a typical swash plate-controlled closed-circuit hydrostatic transmission has been developed. The model has been validated against the experimental data collected on the hydrostatic transmission setup.
Fig. 1 shows the scheme of a typical closed-circuit hydrostatic transmission with a variable displacement pump and a constant displacement motor. The pump and motor flow losses are retrieved by using a boost pump.
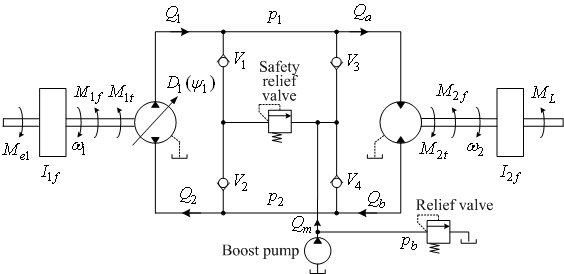
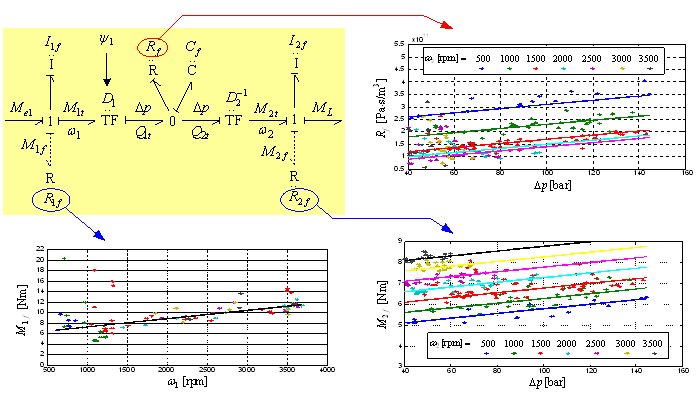
The model development has started from a traditional approach based on two pressure state variables p1,2 (for two working lines) and a separate submodel for the boost pump. Under the assumption that the boost pump flow may be included in the overall flow loss resistance empirical model, the traditional model is reduced to a model including only one pressure state variable - the pressure difference Δp = p1 - p2. The bond graph form of the reduced model is shown in Fig. 2. The model is of third order, where the state variables are pressure difference Δp, the pump speed ω1, and the motor speed ω2. Experimental identification has been used to create the maps for the flow loss resistance parameter Rf, and the pump and motor torque losses M1,2f (Fig. 2).
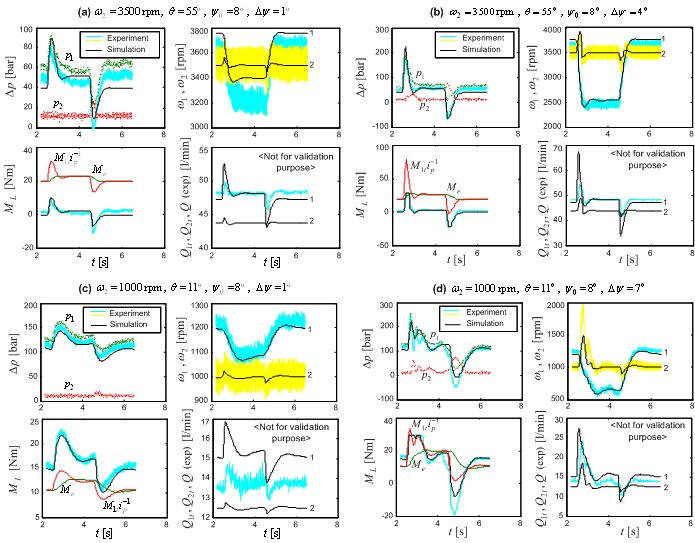
The characteristic experimental validation results are shown in Fig. 3 for the hydromotor speeds ω2 = 3500 rpm and ω2 = 1000 rpm, and for both small and large signal operating modes (small and large swash plate angle steps Δψ). These results (and many other validation results not shown herein) indicate that the relatively simple, third-order nonlinear model can provide an accurate description of the most dominant/relevant effects of hydrostatic transmission dynamics.
More details on the model development, as well as its application on modeling of a typical hydrostatic torque vectoring differential, can be found in our publications listed below.