Road Condition Estimation
The information about road condition is an important aspect of driving safety, because it relates to maximum available tire-road forces. The road condition estimation can be based on utilization of specialized sensors such as optical sensors (i.e. for detection of road texture), or acoustic or strain-gauge sensors built into the tire. However, the tire/road friction estimators are more commonly based on standard automotive sensors and appropriate models of powertrain, driven wheel and/or vehicle for the case of longitudinal, lateral, or combined vehicle motion. They can be developed for the low-slip or high-slip tire/vehicle operating modes. The main advantage of low-slip road condition estimators is the possibility of estimation of tire friction potential without entering the unstable high-slip operation, thus providing preview information to the driver or an Integrated Vehicle Dynamics Control (IVDC) system. Road condition estimation approaches based on the characteristics of the low-slip tire static curve are based on the experimentally observed dependence of the low-slip tire static curve gradient kt = dμ/ds on the road condition (see illustration in Fig. 1a). The low-slip tire static curve gradient also influences the features of tire torsional vibrations caused by the tire sidewall compliance. These vibrations can be excited by the driver or by the uneven road surface (road noise effect). Fig. 1b shows the two-mass elastic model of the tire torsional vibrations. The road noise effect can be modeled as white noise-like torque component Md, and the tire vibrations at the wheel rim side can be approximately described by the second-order oscillator model G(s) whose damping ratio ζ is inversely proportional to the tire static curve gradient kt.
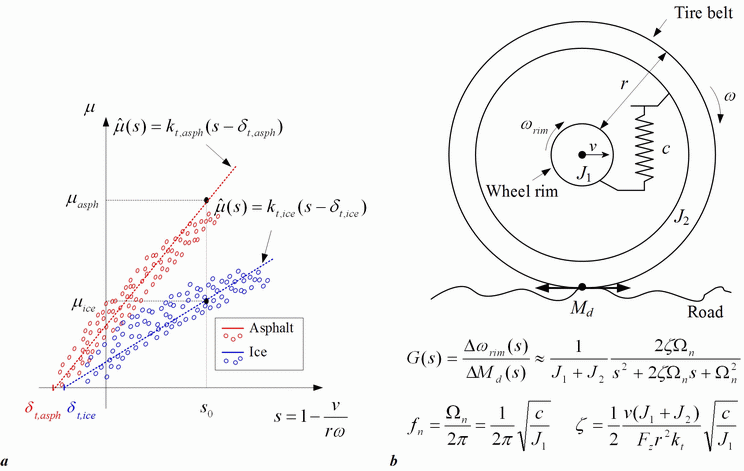
Fig. 1. Illustration of low-slip tire static curves for straight-line driving on asphalt and ice (a), and elastic two-mass tire model (b).
The aforementioned low-slip tire friction effects have been verified experimentally by utilizing a Ford Focus test vehicle equipped with appropriate wheel speed and wheel torque sensors. The comparative experimental tire static curve data μ(s) for different types of road surfaces are shown in Fig. 2a. They are approximated in the least-squares sense by second-order polynomials. The experimental results in Figs. 2a and 2b indicate that the zero-slip static curve gradient kt for dry concrete is 5-8 times larger compared to wet ice, and 3-5 times larger compared to wet or dry snow. Note also that the gradient values do not overlap over a relatively wide range of low wheel slips, so that the information on low-slip tire static curve gradient can indeed be used for road condition estimation.
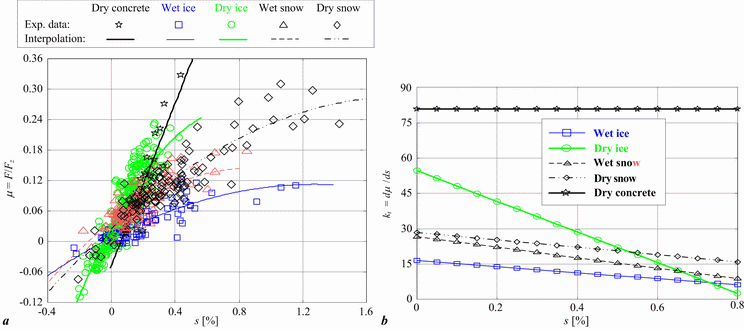
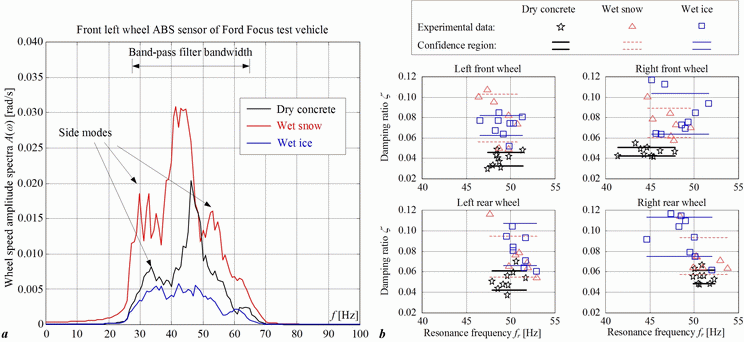
The relationship between the damping ratio of the tire vibration mode at 40 Hz and the road condition has also been experimentally verified. The results are shown in Fig. 3. The amplitude spectra of band-pass filtered wheel speed signals in Fig. 3a clearly indicate the tire vibration mode resonant peaks located at approximately 40 Hz (band-pass filtering is applied in order to extract the interesting tire vibration mode at 40 Hz). The 40 Hz vibration model parameters (the damping ratio ζ and the resonance frequency fn in Fig. 1b) have been estimated off-line by utilizing the instrumental variable least-squares estimation approach. The estimation results shown in Fig. 3b indicate that larger values of damping ratio ζ are obtained for road conditions characterized by smaller tire static curve gradients and vice versa (cf. Fig. 2b and Fig. 3b). However, the estimated damping ratio ζ is not ideally inversely proportional to the tire static curve gradient kt (cf. Fig. 1b), which may be explained by the relatively low road noise excitation, and the distortion of 40 Hz mode due to its overlap with other tire modes (see Fig. 3a).
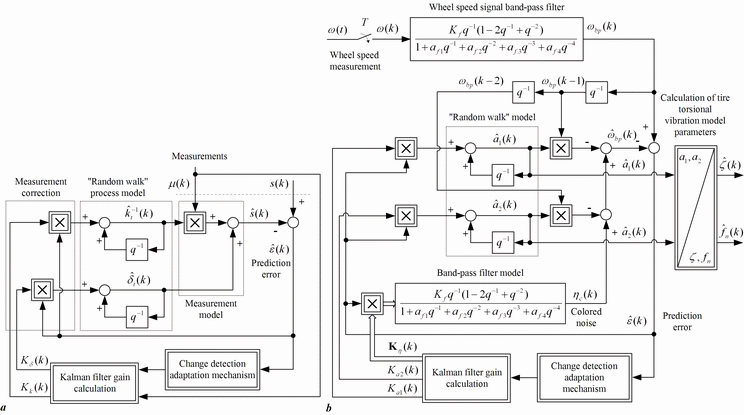
On-line estimation of road condition is based on adaptive Kalman filter approach. For the purpose of adaptive Kalman filter design, the variations of tire static curve and tire vibration model parameters are modeled by the so-called "random-walk" stochastic model. The block diagrams of the proposed road condition estimators are shown in Fig. 4. Note that the adaptive Kalman filter for the estimation of tire vibration model parameters includes a band-pass filter used to extract the 40 Hz vibration mode from the wheel speed signal &omega (Fig. 4b).
The results of experimental verification of the proposed adaptive Kalman filter-based road condition estimators for the case of transition form dry concrete to wet ice are shown in Fig. 5a. The comparative experimental responses in Fig. 5a show that the application of adaptive Kalman filter results in a relatively fast response of the estimated gradient parameter kt compared to the non-adaptive Kalman filter (the effective response delay of the adaptive Kalman filter is 250 ms). The results of estimation of tire vibration model parameters in Fig. 5b show that the band-pass filtered wheel speed signal (estimator input) is characterized by a notable increase of 40 Hz mode magnitude, due to a bump at the transition between concrete and ice. This sudden increase in 40 Hz mode excitation facilitates rather fast estimator response even in the case of non-adaptive Kalman filter (50 ms response time is obtained), compared to the more complex adaptive Kalman filter.
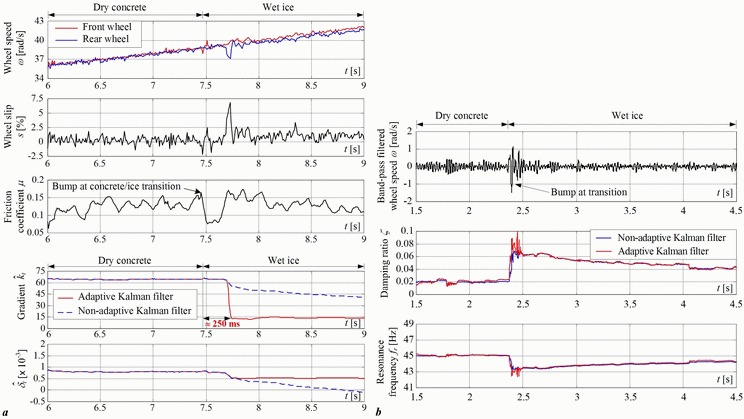
Based on the above results, it can be concluded that the tire static curve gradient-based estimator is characterized by good discrimination between concrete and ice, but it requires the measurement/reconstruction of tire friction coefficient μ and the wheel slip s. On the other hand, the tire torsional vibrations model-based estimator requires the wheel speed measurement only, but the discrimination between road surfaces is less accurate.
Publications
-
SAE paper #2008-01-0585, SAE International Journal of Passenger Cars - Mechanical Systems, Vol. 1, No. 1, pp. 480-491, 2008. -
Experimental Analysis of Potentials for Tire Friction Estimation in Low-Slip Operating Mode
SAE paper #2006-01-0556, SAE Transactions Journal of Passenger Cars - Mechanical Systems, Vol. 115, No. 6, pp. 369-380, 2006. -
Estimation of Tire Static Curve Gradient and Related Model-based Traction Control Application
Proc. of 2009 IEEE Multi-conference on Systems and Control, St. Petersburg, Russia, 2009. -
On Low-slip Tire Friction Behavior and Modeling for Different Road Conditions
CD Proceedings of XIX IAVSD Symposium, Milan, Italy, 2005. -
State Estimation of Automotive Drive with Control Applications [open access]
Doctoral thesis (in Croatian), Faculty of Mechanical Engineering and Naval Architecture, University of Zagreb, Croatia, 2007.