Torque Estimation

SI engine load torque can be regarded as a disturbance variable, which is usually estimated as a difference between the developed engine torque M_m (usually reconstructed from the engine intake manifold pressure and the engine speed measurements) and the low-pass filtered derivative of engine momentum (inertia x speed) J(dω/dt)_F. Thus obtained load torque signal can be directly applied in different powertrain/drivetrain control systems, such as automatic transmission control, engine torque control, idle speed control (ISC) with feedforward load torque compensation, and traction control.

The utilization of more advanced load torque estimator structures should result in more accurate load torque estimation with favorable signal-to-noise ratio. A natural load torque estimation approach would be the Luenberger estimator of load torque disturbance variable. However, due to the measurement noise constraints, tuning of the Luenberger estimator is usually a trade-off between the estimator response speed and favorable signal-to-noise ratio. In order to overcome these constraints, an adaptive Kalman filter has been developed. It is based on a simple stochastic state-space model of engine rotational dynamics shown in Fig. 1.

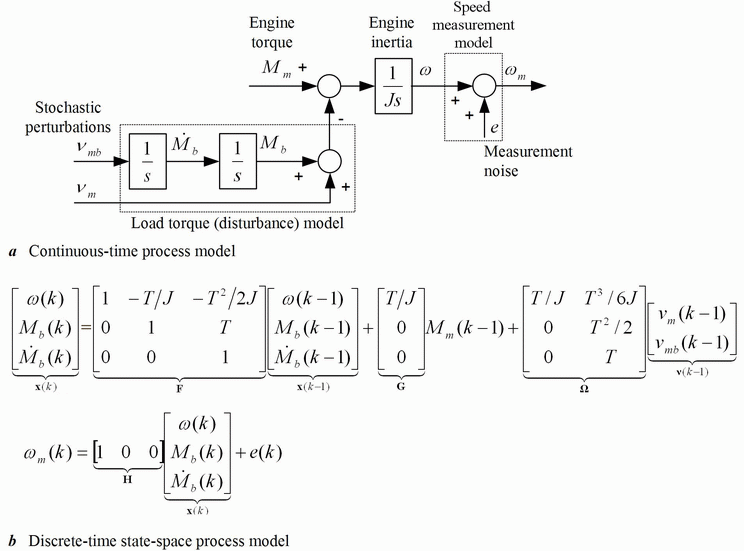
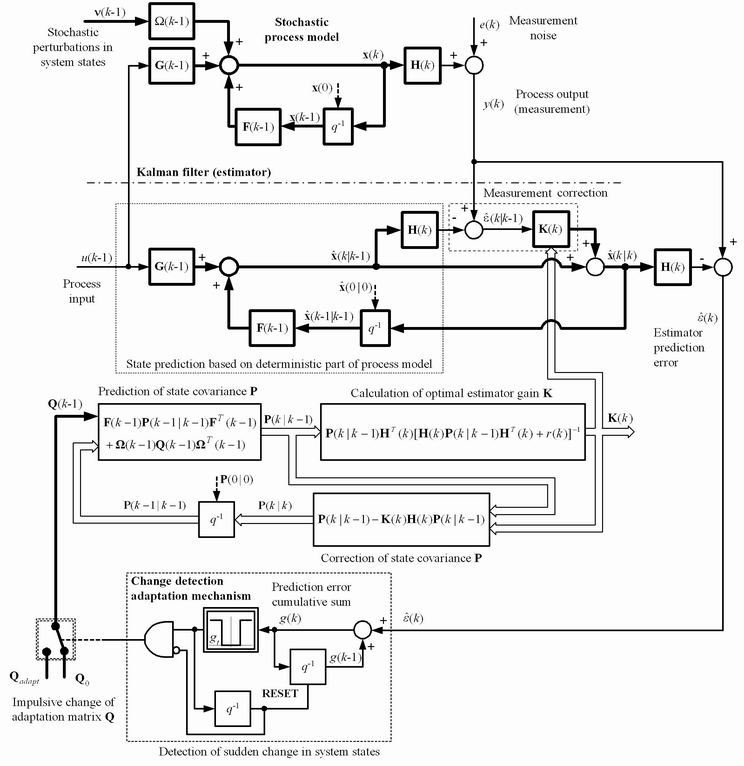
The block diagram of the adaptive Kalman filter for a discrete-time Single-Input / Single-Output (SISO) process model is shown in Fig. 2. It comprises the deterministic part of the process model whose estimated state variables are corrected by means of measurements. The Kalman filter feedback gains (matrix K) are calculated based on the assumed properties (co-variances Q) of stochastic perturbations in the system state variables. In order to improve the estimator response speed for the case of sudden state variable changes (i.e. abrupt engine load torque changes), while preserving favorable steady-state noise suppression ability, the Kalman filter is extended with an adaptation mechanism. The adaptation is based on load torque change detection by means of monitoring of the estimator prediction error cumulative sum, and on-line adaptation of the Q matrix.

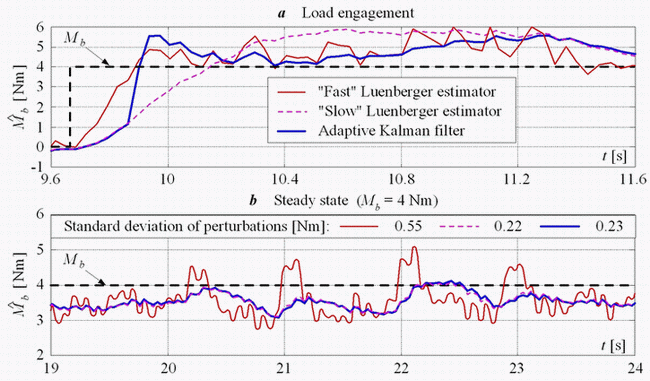
The adaptive Kalman filter and Luenberger estimator have been compared by means of experiments, carried out on the experimental setup of a 14 HP V2 SI engine within the framework of idle speed control. On the particular SI engine setup, the engine speed is directly measured, while the developed engine torque is reconstructed from the intake manifold pressure signal. The results of comparative experimental analysis in Fig. 3 show that the application of adaptive Kalman filter results in a favorable signal-to-noise ratio in the estimated engine load torque signal comparable to Luenberger estimator tuned for slow response, while achieving a load torque response speed comparable to the Luenberger estimator tuned for fast response. Note, however, that the initial part of the adaptive Kalman filter response has slower rate compared to the fast Luenberger estimator, because the adaptation mechanism requires some time to be triggered. After the load torque change is detected, the response of adaptive Kalman filter is sped-up, and step response risetime and settling time become comparable to the fast Luenberger estimator. The relatively small steady-state load torque estimation offset of 0.5 Nm (approx. 2% of rated torque for the particular engine) is due to a certain inaccuracy of the manifold pressure-based engine torque reconstruction.

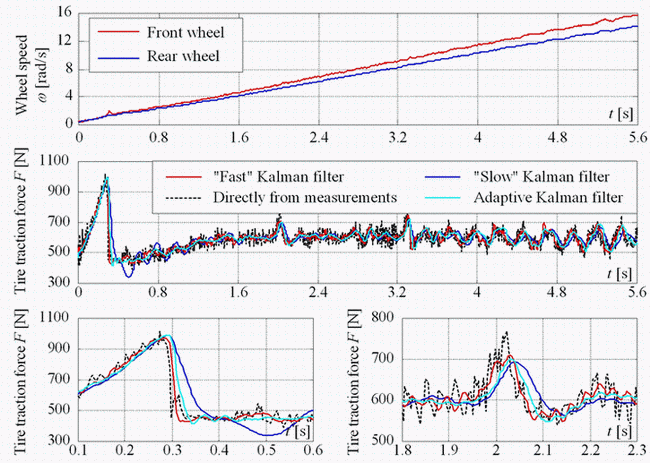
The adaptive Kalman filter approach can also be used for tire traction force estimation assuming that the wheel speed measurement is available (from ABS sensor) and that the wheel torque can be reconstructed either from in-wheel motor current measurement (in the case of an electrical vehicle), or from a drivetrain model in the case of a traditional vehicle. The experimental results of tire traction force estimation within the traction control system of the experimental electrical vehicle for the case of 10% wheel slip target are shown in Fig. 4. The estimator responses illustrate the advantages of adaptive Kalman filter for tire traction force estimation. The adaptive Kalman filter is able to capture fast changes of tire friction force with the response speeds similar to fast non-adaptive Kalman filter, while maintaining good suppression of noise (comparable to slow non-adaptive Kalman filter).