Modeliranje dinamike aktivnih diferencijala
Aktivni diferencijali omogućuju upravljanje distribucijom momenta na pojedine kotače, s ciljem unaprjeđenja karakteristika regulacije vuče i regulacije dinamike vozila bez nametljivog djelovanja kočnica. Aktivni diferencijali mogu se podijeliti u dvije skupine: aktivni diferencijal s ograničenim proklizavanjem (poluaktivni diferencijali) i puni aktivni diferencijali s usmjeravanjem prijenosnog momenta. U svrhu sinteze i simulacije sustava regulacije dinamike vozila, razvijen je i analiziran unificirani matematički i simulacijski model dinamike pogona vozila s raznim tipovima aktivnih diferencijala.
Slika 1 prikazuje kinematske sheme četiri uobičajena tipa aktivnih diferencijala. Poluaktivni diferencijal (Sl. 1a) sadrži spojku koja spaja rotirajuće kućište diferencijala s jednim od izlaznih vratila. Budući da se moment spojke uvijek usmjerava od bržeg prema sporijem vratilu i budući da je brzina vrtnje kućišta jednaka srednjoj brzini izlaznih vratila (kotača), poluaktivni diferencijal uvijek prenosi moment sa bržeg na sporiji kotač. Puni aktivni diferencijali (Sl. 1b-1d) sadrže dvije spojke i dodatne zupčanike, kako bi omogućio prijenos momenta na sporiji i brži kotač. Dopuštena razlika brzina vrtnje kotača za prijenos momenta sa sporijeg na brži kotač određena je ekvivalentnim prijenosnim omjerom dodatnih zupčanika, te se tipično nalazi u rasponu od 10% do 25%. Spojke mogu biti rotirajuće (Sl. 1b) ili stacionarne (Sl. 1c,d). Aktivni diferencijal za pogon na četiri kotača (Sl. 1d) koristi se kao aktivni stražnji diferencijal koji se spreže s pasivnim (otvorenim) prednjim diferencijalom. Sprezanje se u aktivnom modu ostvaruje pomoću zupčaničkog mehanizma za podizanje brzine vrtnje stražnjeg diferencijala.
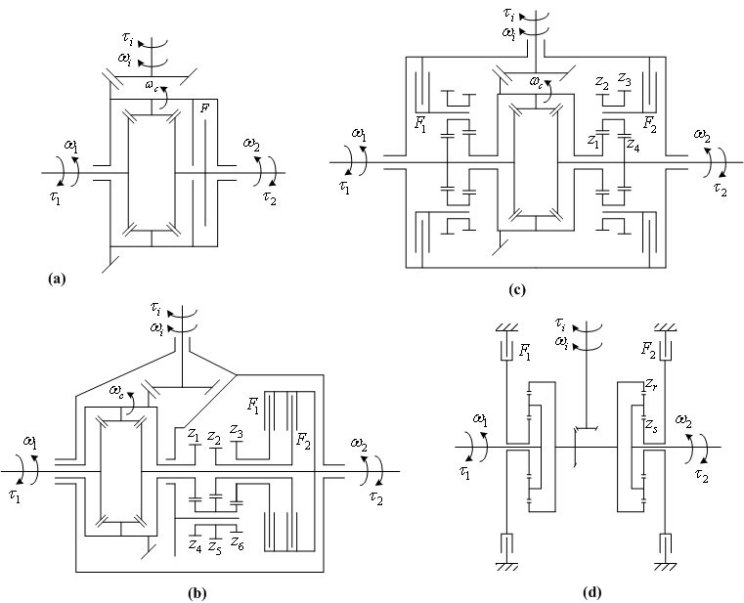
Sl. 1. Kinematske sheme aktivnih diferencijala: (a) poluaktivni diferencijal, (b) aktivni diferencijal s rotirajućim spojkama, (c) aktivni diferencijal sa stacionarnim spojkama i (d) aktivni diferencijal za pogon na četiri kotača.
Slika 2 prikazuje vezni dijagram modela dinamike pogona s gore opisanim diferencijalima.
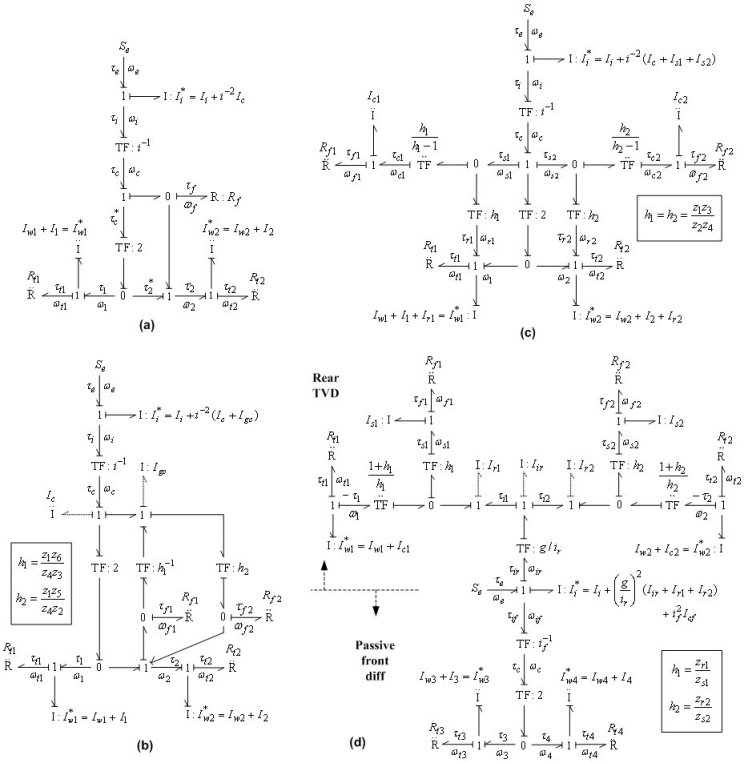
Postavljanjem jednoznačne kauzalnosti tipa "momenta" za otporne elemente trenja autogume Rti (i = 1,2 ili i = 1,...4) i spojke Rf1,2, te integralne kauzalnosti za inercije kotača Iwi*, pokazuje se da ulazna inercija Ii* (i eventualne preostale inercije) ima derivativnu kauzalnost. Dakle, ukupni model je drugog reda za pogon na dva kotača, odnosno četvrtog reda za pogona na četiri kotača, te je dan sljedećim unificiranim skupom jednadžbi:
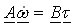
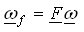
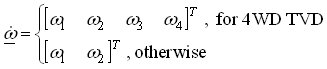
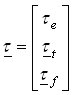
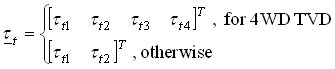
i gdje inercijska matrica A, ulazna matrica B, i matrica transformacije brzine vrtnje F ovise of tipu diferencijala. Numerička integracija gore dane jednadžbe stanja daje vektor brzine vrtnje kotača ω, i zahtijevani vektor momenta spojki ωf. Vektor brzine spojki ωf i zahtijevani vektor momenta spojki τh koriste se za proračun vektora momenata trenja spojki τf, koji se zajedno s ulaznim momentom τe i vektorom momenta tereta kotača τt vraća kao povratna informacija u linearni model stanja. Slika 3 ocrtava implementaciju modela na temelju Karnoppovog modela trenja spojki. Linearni model diferencijala dan je gore navedenim jednadžbama. Model trenja spojki zasniva se na poopćenoj Stribeckovoj statičkoj krivulji trenja i primijenjenom momentu spojki τstick koji se računa u podsustavu Model statičkog trenja. Model se može lako proširiti učincima elastičnosti poluvratila i pojedinačnih inercija diferencijala.
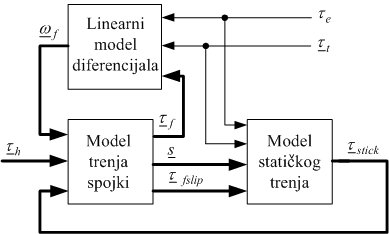
Razvijeni model primijenjen je za usporednu algebarsku i simulacijsku analizu dinamike pogona s aktivnim diferencijalima. Vibracijska analiza pokazuje da su karakteristike vibracijskog moda pobuđenog od strane ulaznog momenta slične za sve diferencijale. S druge strane, vibracijski mod pobuđen aktiviranjem spojke može imati nepovoljna niskofrekvencijska svojstva za aktivni diferencijal sa stacionarnim spojkama, jer inercija spojke i zupčanika postaje razmjerno velika kada se svede na izlazno vratilo diferencijala preko visokog ekvivalentnog prijenosnog omjera zupčanika. Analiza vremenskih odziva ukazuje da poluaktivni diferencijal, pored nedostatka prijenosa momenta samo na sporiji kotač, ima i spor i/ili stacionarno netočan odziv prijenosnog momenta za vrlo male razlike brzina vrtnje kotača.
Podrobnije informacije o razvoju modela za različite konfiguracije pogona, analizi stacionarnog i dinamičkog ponašanja pogona i simulacijskim rezultatima mogu se naći u referencama danim dolje.
Publikacije
-
Encyclopedia of Automotive Engineering, pp. 1-19, John Wiley & Sons Ltd., 2014. -
Bond Graph Modeling of Automotive Transmissions and Drivelines
Proc. of 7th Vienna International Conference on Mathematical Modelling (MATHMOD), Vienna, Austria, 2012. -
Modeling and Analysis of Active Differential Dynamics
ASME Journal of Dynamic Systems, Measurement, and Control, Vol. 132, No. 6, pp. 061501/1-13, 2010. -
A Closed-Loop Strategy of Active Differential Clutch Control
ASME Dynamic Systems and Control Conference (2009 DSCC), Hollywood, CA, 2009. -
Modelling and Analysis of Torque Vectoring Differential Kinematics
Proc. of the 6th International Congress of Croatian Society of Mechanics, Dubrovnik, Croatia, 2009. -
Bond Graph Modeling and Analysis of Active Differential Kinematics
2008 ASME Dynamic Systems and Control Conference, Ann Arbor, MI, 2008. -
Experimental Setups for Active Limited Slip Differential Dynamics Research
SAE paper #2008-01-0302, 2008 SAE World Congress, Detroit, MI, 2008. -
Modeling of Active Differential Dynamics
DVD Proc. of 2008 ASME International Mechanical Engineering Congress and Exposition (IMECE 2008), Boston, MA, 2008. -
A Control-oriented Model of Hydrostatic Transmission with Application on Torque Vectoring Differential Modeling
DVD Proc. of 2008 ASME International Mechanical Engineering Congress and Exposition (IMECE 2008), Boston, MA, 2008.